在神经网络中,激活函数sigmoid和tanh除了阈值取值外有什么不同吗?
讨论这两个函数本身的话,除了平移和拉伸以外,本质上没区别。
但是不知道激活函数对这两个操作是否敏感
bengio deep learning书6.3.2节:
When a sigmoidal activation function must be used, the tanh activation function typically performs better than the logistic sigmoid It resembles the identity function more closely.
大意是tanh更接近y=x,所以比sigmoid好。后面还有一句解释,符号太多,大意是tanh过原点,而sigmoid不过,而且因为tanh在原点附近与y=x函数形式相近,所以当激活值较低时,可以直接进行矩阵运算,训练相对容易。
这个问题之前我也没想太清楚,看了斯坦福 cs231n 的课程后,稍稍领会了一些,在这里交流下:
从数学上看,这两个函数可以通过线性变化等价,唯一的区别在于值域是 (0,1) 和 (-1, 1)。
作为激活函数,都存在两端梯度弥散、计算量大的问题,sigmoid函数因为和生物上的神经元信号刺激的 firing rate 长得像,一度比较流行。。。
但是,作为非中心对称的激活函数,sigmoid有个问题:输出总是正数!!!
这意味着,神经网络的隐层每个节点的输出(activation)总是正数(注:bias可以看做activation为+1),会导致什么问题?看下图(请忽略粗糙程度 ):
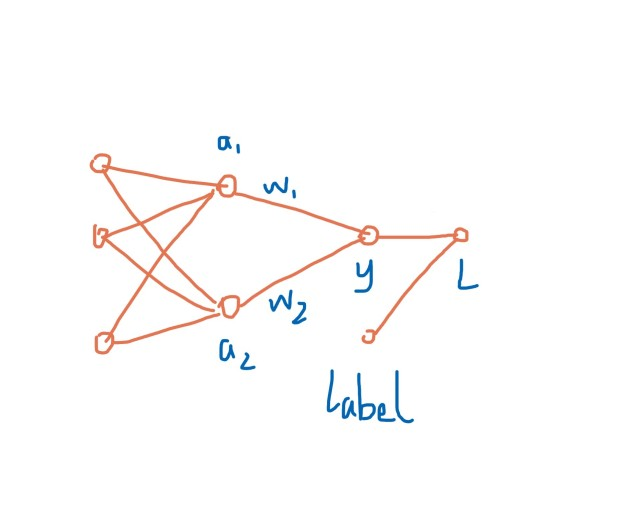
其中因为激活函数使用 sigmoid, a1>0, a2>0,对上图应用链式法则求 w1、w2偏导:
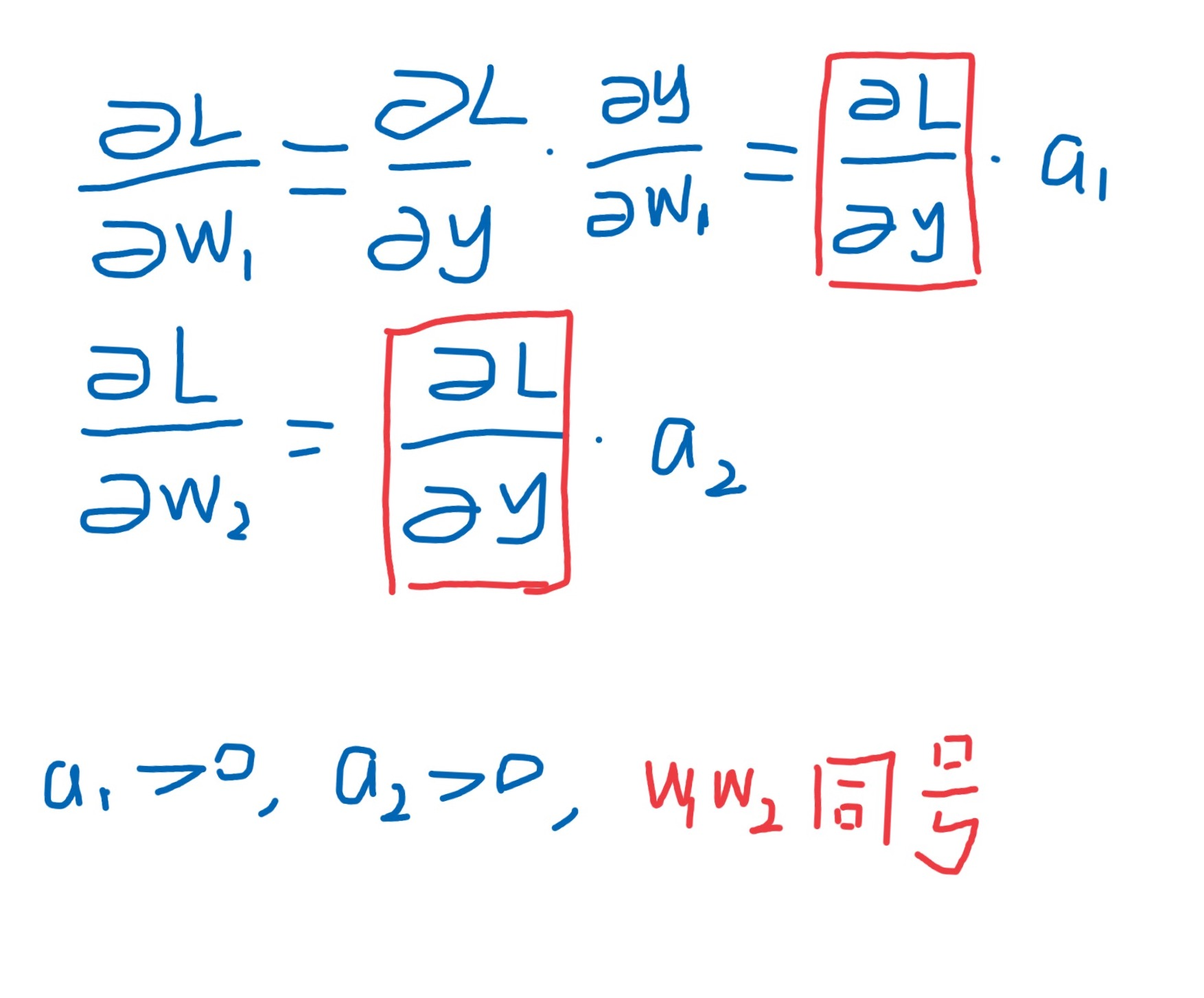
得出结论,w1、w2的梯度方向均取决于同一个值,意味着,(w1,w2)梯度必须在第一和第三象限方向移动,如果生不逢时,初始值没那么幸运,优化路径容易出现zigzag现象,汇总到 cs231 的一张ppt里,就是这样:

最后,如果还想了解更多,可以看看视频:斯坦福2017季CS231n深度视觉识别课程视频(by Fei-Fei Li, Justin Johnson, Serena Yeung)(英文字幕)
在比较sigmoid和tanh函数之前,先将两个函数画在下面:
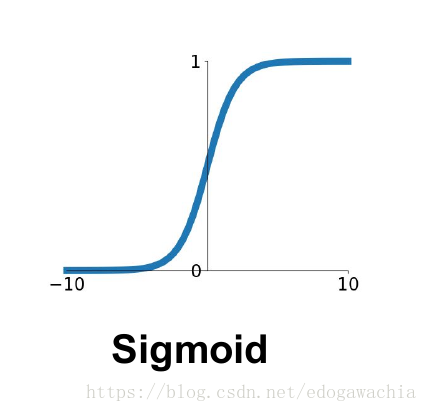
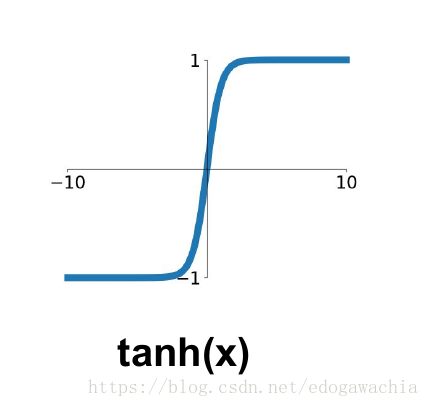
从上面的图看到tanh函数像是伸缩过的sigmoid函数然后向下平移了一格,确实就是这样,因为它们的关系就是线性关系,即
从公式看出,其实tanh函数就是sigmoid沿x轴缩小一倍,沿y轴伸展一倍,然后平移一格得到的,所以它们注定有很多相似点。
1.有饱和区,在输入较大或较小的地方,梯度变为0,神经元无法更新
2.都有指数运算,运算量很大
以上主要是两者相似的地方,但是两者也存在不同之处。
首先,提到激活函数,经常会提到是否是以零为中心的,如图所示,我们看出tanh函数是以零为中心的,sigmoid函数则不是,那么是否以零为中心对训练有什么影响呢?
如果激活函数为sigmoid时(不以零为中心),那么输出的值大于0,那么根据链式法则,后向传播跨层求w的局部梯度如下式:
其中 ,
,
,因此上式的梯度主要取决于x的符号,而x在输入层可能有正有负,但是在隐藏层中经过sigmoid激活函数后全为正数,因此,隐藏层w的更新要么全部往负向走,要么全部正向走(取决于最后一层
传递上来的值),假如权重为二维,那么全为负的和全为正的权重相加分布在一三象限,因此会出现zigzag现象,导致收敛速度缓慢。如下图所示:
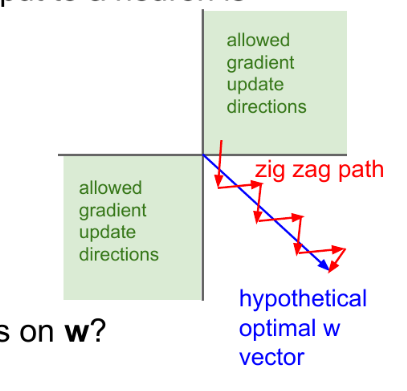
因此,以零为中心的激活函数不会出现zigzag现象,因此相对来说收敛速度会变快。
这篇博客说的比较好,直接拿了过来
1.首先尝试ReLU,速度快,但小心设置 learning rate,注意不要让网络出现很多 “dead” 神经元
2.如果ReLU效果欠佳,尝试 Leaky ReLU、PReLU 、Maxout 或者 ELU函数
3.sigmoid、tanh 常应用在RNN(LSTM、注意力机制等),作为门控或者概率值
4.很少会把各种激活函数串起来在一个网络中使用
5.在ResNet 50上测试,同等条件下,性能对比 ReLU > RReLU > SELU(1.0) >ELU(1.0)=LeakyReLu(0.1) > LeakyReLu(0.2) > PReLU
参考内容
1.cs231n课程
2.https://blog.csdn.net/WJ_MeiMei/article/details/89317972
完整的各种常见激活函数介绍详见 深入理解深度学习中常见激活函数
sigmoid激活函数被广泛使用,和生物神经元的激活逻辑最接近,其定义如式子(4)所示,函数图像如图3所示。
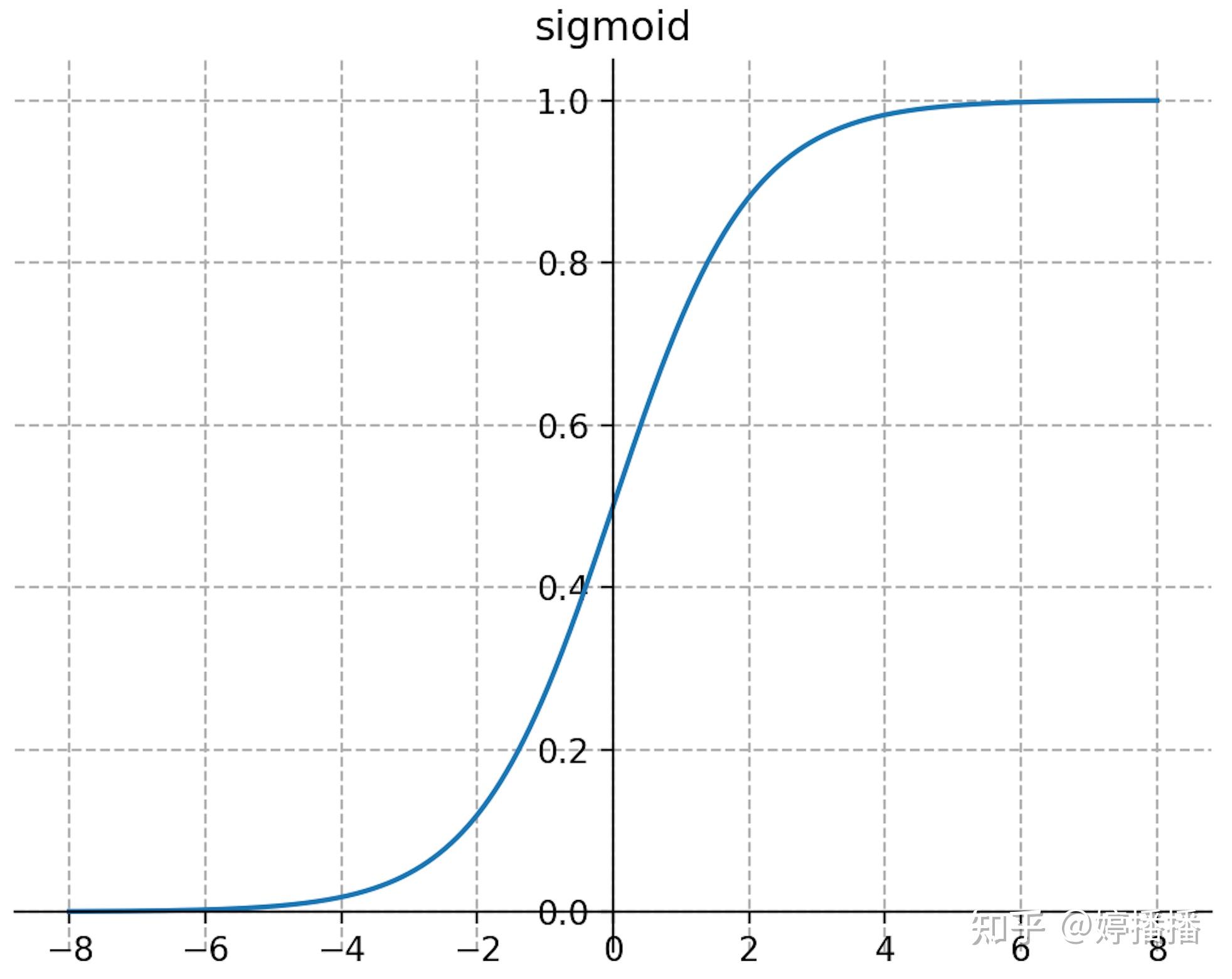
sigmoid函数的特点明显:(1) 连续光滑、严格单调;(2) 输出范围为(0,1),以(0, 0.5)为对称中心;(3) 当输入趋于负无穷时,输出趋近于0,当输入趋于正无穷时,输出趋近于1;(4) 输入在0附近时,输出变化趋势明显,输入离0越远,变化趋势越平缓且逐渐趋于不变。
根据sigmoid激活函数的特点,可以得到对应的优缺点。其优点包括:(1) 输出范围为(0,1),适合作为概率的使用;(2) 求导方便,如式子(5)所示,不需要额外的计算量。
其缺点包括:(1) 当输入离0较远时,输出变化非常平缓,容易陷入梯度饱和状态,导致梯度消失问题;(2) 以(0, 0.5)为对称中心,原点不对称,容易改变输出的数据分布;(3) 导数取值范围为(0, 0.25](推导过程见式子(5)),连乘后梯度呈指数级减小,所以当网络加深时,浅层网络梯度容易出现梯度消失,详细原因见推导1;(4) 输出总是正数,使反向传播时参数w的梯度全正或全负,梯度下降出现zigzag形状,导致网络收速度慢,详细原因见分析1;(5) 计算包括指数项,耗时多。
推导1 sigmoid激活函数梯度消失问题
根据梯度反向传播式子(2.2)有 ,而根据sigmoid的求导式子(5)有
,w一般会进行标准化,因此w通常小于1,所以得到
,可以看出,损失对y的梯度随着层数的增加按照每层1/4的大小缩小,当深度较深时,损失对y的梯度容易变得很小甚至消失。
根据式子(2.1)有 ,参数w的梯度依赖于y的梯度,当损失对y的梯度消失时,参数w的梯度也随之消失,从而造成梯度消失问题。
分析1 sigmoid激活函数zigzag现象
1 参数w的梯度方向特点
参数w的梯度为 ,由于sigmoid的导数
恒为正,y为上一层隐层经过sigmoid的输出,同样恒为正,因此参数w的梯度方向取决于
的梯度方向,而对同一层的所有参数w而言,
是相同的,所以同一层的参数w在更新时要么同时增大,要么同时减小,没有自己独立的正负方向。
2 为什么参数的梯度方向一致容易造成zigzag现象
当所有梯度同为正或者负时,参数在梯度更新时容易出现zigzag现象。zigzag现象如图4所示,不妨假设一共两个参数, 和
,紫色点为参数的最优解,蓝色箭头表示梯度最优方向,红色箭头表示实际梯度更新方向。由于参数的梯度方向一致,要么同正,要么同负,因此更新方向只能为第三象限角度或第一象限角度,而梯度的最优方向为第四象限角度,也就是参数
要向着变小的方向,
要向着变大的方向,在这种情况下,每更新一次梯度,不管是同时变小(第三象限角度)还是同时变大(第四象限角度),总是一个参数更接近最优状态,另一个参数远离最优状态,因此为了使参数尽快收敛到最优状态,出现交替向最优状态更新的现象,也就是zigzag现象。
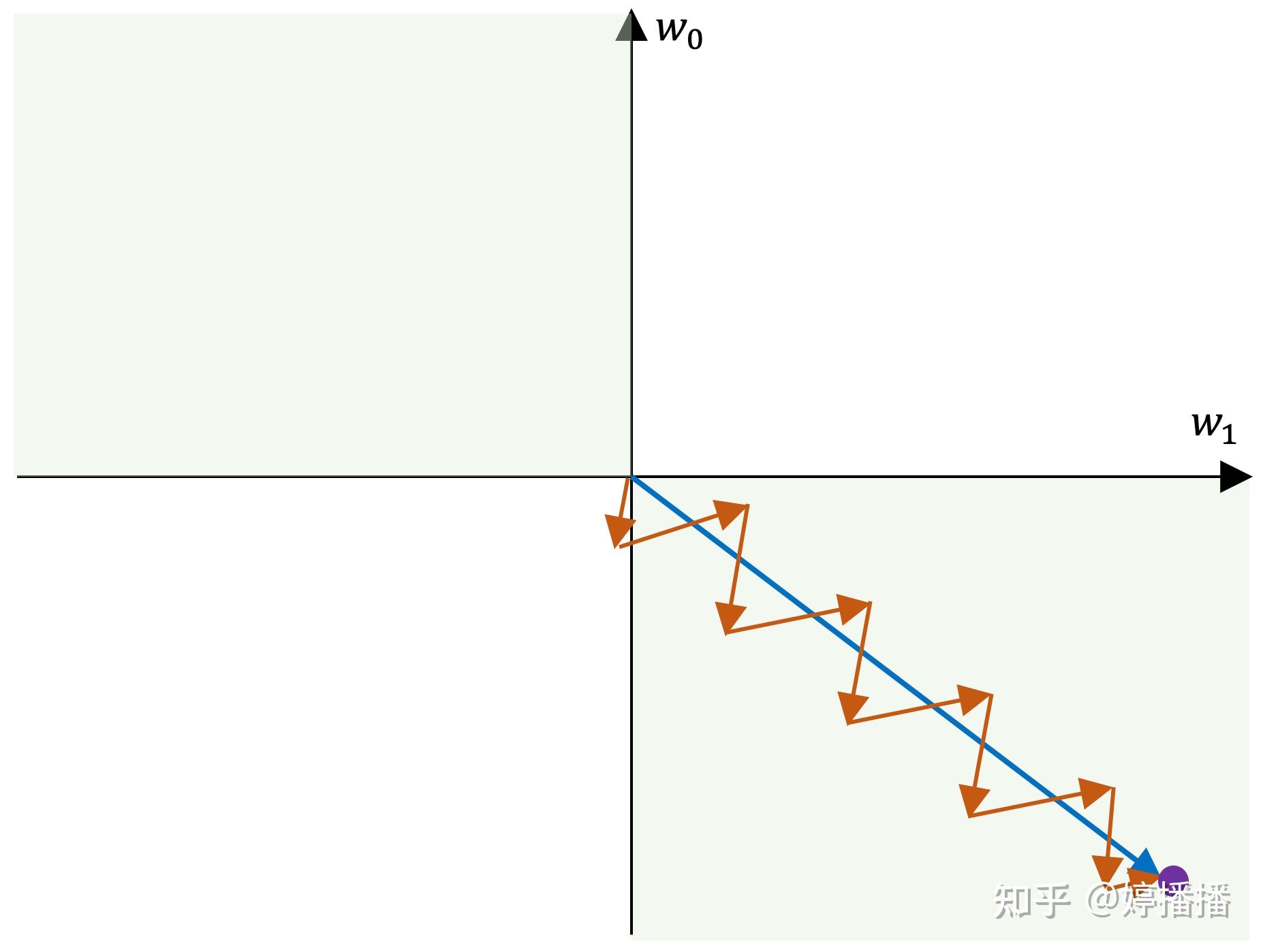
sigmoid函数在什么情况下会出现zigzag现象呢(有兴趣的朋友可以先思考一下再看后面的内容)。从上面的分析可以看出,当梯度更新的最优方向不满足所有参数梯度正负向一致时,也就是有的参数梯度正向,有的参数梯度负向,容易出现zigzag现象。
两个参数时,出现zigzag现象的梯度更新最优方向为图4中的绿色背景部分,即第二象限和第四象限。在深度学习中,网络参数非常巨大,形成高维的空间,梯度更新的最优方向非常容易出现不同参数的梯度正负向不一致的情况,也就更容易造成zigzag现象。
抛开激活函数,当参数量纲差异大时,也容易造成zigzag现象,其中的原因和sigmoid函数造成的zigzag现象,是相通的。
tanh激活函数如式子(6)所示,函数图像如图5所示。
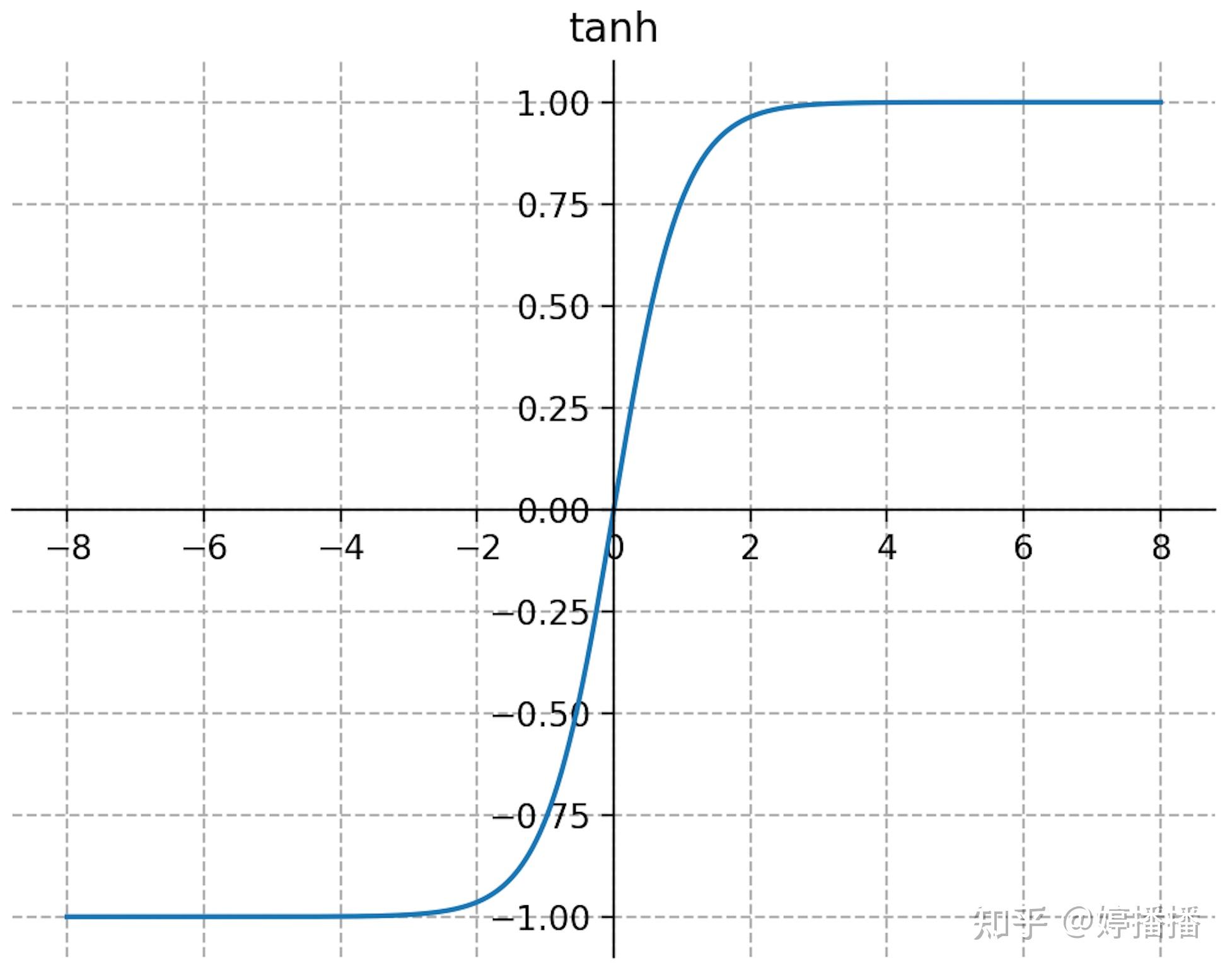
tanh函数形状和sigmoid函数很相似,由tanh和sigmoid函数的定义有 ,因此tanh函数可以由sigmoid函数伸缩平移得到,所以tanh函数一些特点和sigmoid函数相同。
tanh函数特点:(1) 连续光滑、严格单调;(2) 输出范围为(-1,1),以(0, 0)为对称中心,均值为0;(3) 输入在0附近时,输出变化明显;输入离0越远,输出变化越小最后输出趋近于1不变。
根据tanh函数的特点可以得到其优缺点。
优点:输出关于原点对称,0均值,因此输出有正有负,可以规避zigzag现象,另外原点对称本身是一个很好的优点,有益于网络的学习。
缺点:存在梯度消失问题,tanh的导数计算为 ,取值范围为(0,1],虽然取值范围比sigmoid导数更广一些,可以缓解梯度消失,但仍然无法避免随着网络层数增多梯度连乘导致的梯度消失问题。
推荐系列文章:
推荐模型结构-特征交叉
- ctr模型特征交叉结构总结与业务应用和思考
- xDeepFM如何实现field-wise显式高阶特征交叉-模型结构之特征交叉(3)-DCN系列之xDeepFM(3.3)附代码
- DCN-V2对特征交叉做了什么改进--模型结构之特征交叉(3)-DCN系列之DCN-V2(3.2)附代码
- 为什么DCN可以实现显式高阶特征交叉-模型结构之特征交叉(3)-DCN系列(3.1)附代码
- 模型结构之特征交叉(2)-FM系列(2.2)-AFM,DeepFM等(附代码)
- 模型结构之特征交叉(2)-FM系列(2.1)-FM,FFM
- 模型结构之特征交叉(1)-从LR到wide&deep
推荐基础知识点
工具
工作相关的内容会更新在【播播笔记】公众号,欢迎关注
生活的思考和记录会更新在【吾之】公众号,欢迎关注
热门文章排行
- 世界十大假戏真做的电影排行榜 真枪实弹太
- 共享,正从风口到风险
- 走进涂料市场的秘密
- 在人工智能炒热机器人时,也被人把风带进了
- 生物涂料有什么好处?
- 智能音箱,正走在智能手表的老路上
- “去乐视化”之后,新易到的机会在哪儿?
- 日本十大波涛汹涌巨乳美少女第5名,凶悍!
- 揭开芽笼神秘面纱
- 菜刀材质的3铬钢、5铬钢、9铬钢,差别有
最新资讯文章
- CSS Navigation Bar
- 高考成绩口语合格是什么意思
- 高中物理动力学常见知识点及公式总结
- 2017新人教版部编人教版二年级语文语文
- DOTA2比分
- 2023年零食带货人气主播TOP10揭晓
- 商务部:4月以来电商平台外贸专区销售额超
- 推荐5款主流的私家车小件接单app,帮助
- 英文很蹩脚?如何找到优质的外包写手?怎么
- 2025年中国生物医药产业链图谱及投资布
- 如何打拼音时加上声调?
- 抖音电商618数据发布:超6万个品牌成交
- 物流外包是什么意思_1
- 中国电竞酒店行业现状分析与投资前景预测报
- 长治医学院2021年全日制普通本科招生章
- 书卷一梦_2
- 未成年将禁止参加电竞赛事?网游新规下电竞
- [官方资料]NVIDIA Jetson
- 苏丹伊德理斯教育大学 | 马来西亚苏丹伊
- 2023版美国留学行前准备指南 | 入境








