数学中最优化问题的一般表述是求取，使，其中是n维向量，是的可行域，是上的实值函数。

凸优化问题是指是闭合的凸集且是上的凸函数的最优化问题，这两个条件任一不满足则该问题即为非凸的最优化问题。

其中，是 凸集是指对集合中的任意两点，有，即任意两点的连线段都在集合内，直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集，则涉及到闭集的定义，而闭集的定义又基于开集，比较抽象，不赘述，这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。

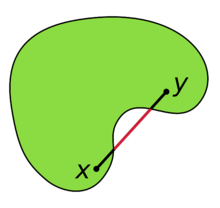
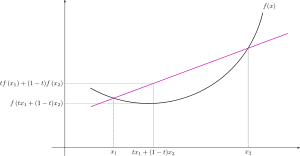
是凸函数是指对于定义域中任意两点，有，直观上就是向下凸出，如下图示意。

实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点：

• 目标函数如果不是凸函数，则不是凸优化问题
• 决策变量中包含离散变量（0-1变量或整数变量），则不是凸优化问题
  
• 约束条件写成时，如果不是凸函数，则不是凸优化问题

之所以要区分凸优化问题和非凸的问题原因在于凸优化问题中局部最优解同时也是全局最优解，这个特性使凸优化问题在一定意义上更易于解决，而一般的非凸最优化问题相比之下更难解决。

资料来自维基，稍有删减改动。

附上wiki链接：

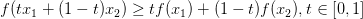
这个公式是不是应该是<=?

楼主我硕士运筹学出身，现在师从德国海德堡大学组合优化教授，TSP鼻祖之一。

1，首先大家需要知道Convex VS Non-Convex的概念吧？

数学定义就不写了，介绍个直观判断一个集合是否为Convex的方法，如下图：

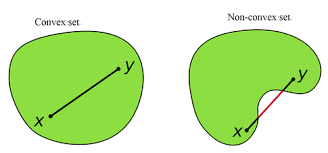
简单的测试一个集合是不是凸的，只要任意取集合中的俩个点并连线，如果说连线段完全被包含在此集合中，那么这个集合就是凸集，例如左图所示。

先补充一点：举几个常见的nonconvex例子，通常2次以上的polynomial不论出现在目标函数或约束条件里，都是noconvex，更不用说什么sin、cos函数了；2次函数在目标函数，如果不是SDP（半正定）的话，也是nonconvex。

2，凸优化-相对简单

凸优化有个非常重要的定理，即任何局部最优解即为全局最优解。由于这个性质，只要设计一个较为简单的局部算法，例如贪婪算法（Greedy Algorithm）或梯度下降法（Gradient Decent），收敛求得的局部最优解即为全局最优。因此求解凸优化问题相对来说是比较高效的。这也是为什么机器学习中凸优化的模型非常多，毕竟机器学习处理大数据，需要高效的算法。

3，非凸优化-非常困难

而非凸优化问题被认为是非常难求解的，因为可行域集合可能存在无数个局部最优点，通常求解全局最优的算法复杂度是指数级的（NP难）。如下图：

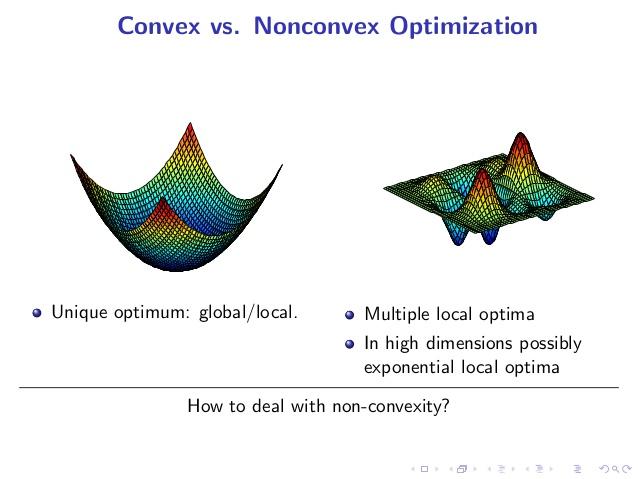
最经典的算法要算蒙特卡罗投点法了，大概思想便是随便投个点，然后在附近区域（可以假设convex）用2中方法的进行搜索，得到局部最优值。然后随机再投个点，再找到局部最优点。如此反复，直到满足终止条件。

假设有1w个局部最优点，你至少要投点1w次吧？并且你还要假设每次投点都投到了不同的区域，不然你只会搜索到以前搜索过的局部最优点。

再补充一点：数学规划模型里面如果有整数变量，这个问题通常被称为 highly nonconvex(极度非凸)，如下图：

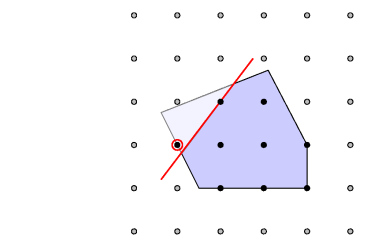
实心黑点组成的集合，是一个离散集，按照1中判断一个集合是否为凸集的技巧，我们很容易验证这个离散集是非凸的。因此整数规划问题也是一个非凸优化问题，并且它也是NP难的。

因此数学规划里最难的一类问题，叫做混合整数非线性规划(mixed integer nonlinear programming)。

那么整数规划的求解思路呢，也遵循了科学研究的本质，即被分解为求解一个个的线性规划问题。感兴趣的朋友可以搜索分支定界法。

举个最简单的例子：
min x_1+x_2^3
s.t. x_1^2-x_2>=2
x_1>=0, x_2 is binary.

预计不久将来会办个关于运筹学、数学规划、数学建模，及其在机器学习、人工智能、数据科学方面的应用的知乎LIVE。
再沉淀段时间。

-----------------------------------

更新，“运筹学”综述Live入口如下：

大数据人工智能时代的运筹学 -- Robin Shen 2017.06.11的知乎Live

以及运筹学、AI专栏 @运筹OR帷幄：

最后按照惯例广告一波：

欧洲、北美、全球留学及数据科学深度私人定制咨询，从此DIY - 知乎专栏

凸优化问题(convex optimization)的定义是目标函数是凸(convex)的，且可行域是凸(convex)的。不符合这个定义的优化问题就是非凸的优化问题(non-convex optimization)，就这么简单~