目录

前言

正文

1 多目标优化概念

2 多目标进化优化算法

3 代码实战

3.1 用NSGA2 优化 ZDT1

3.2 用NSGA3 优化 DTLZ1

3.3 用MOEA/D 优化 ZDT1

3.3 更多的比较

总结

自从上三篇博客详细讲解了Python遗传和进化算法工具箱及其在带约束的单目标函数值优化中的应用、利用遗传算法求解有向图的最短路径、利用进化算法优化SVM参数之后，这篇不再局限于单一的进化算法工具箱的讲解，相反，这次来个横向对比，比较目前最流行的几个python进化算法工具箱/框架在求解多目标问题上的表现。

首先大致讲一下多目标优化：

在生活中的优化问题，往往不只有一个优化目标，并且往往无法同时满足所有的目标都最优。例如工人的工资与企业的利润。那么多目标优化里面什么解才算是优秀的？我们一般采用“帕累托最优”来衡量解是否优秀，其定义我这里摘录百度百科的一段话：

帕累托最优（Pareto Optimality），是指资源分配的一种理想状态。假定固有的一群人和可分配的资源，从一种分配状态到另一种状态的变化中，在没有使任何人境况变坏的前提下，使得至少一个人变得更好。帕累托最优状态就是不可能再有更多的帕累托改进的余地；换句话说，帕累托改进是达到帕累托最优的路径和方法。 帕累托最优是公平与效率的“理想王国”。是由帕累托提出的。

这段话好像让人看着依旧有点懵逼，下面直接摘录一段学术性的定义：

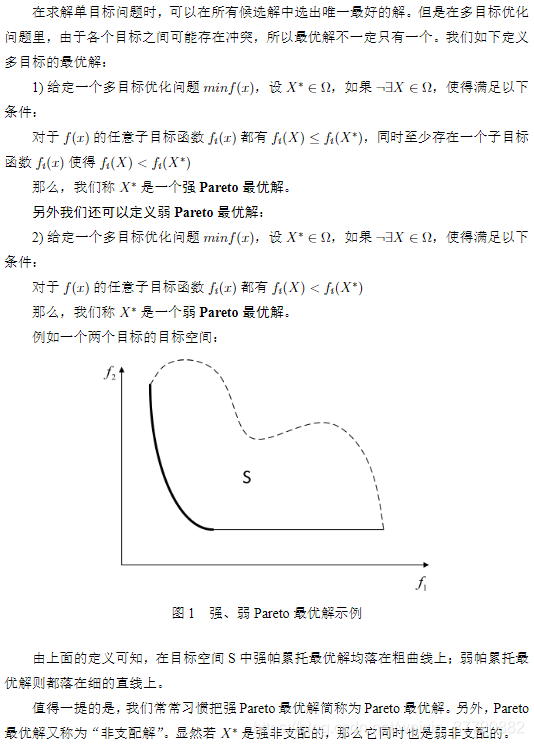
【摘自：Geatpy】

因此，只要找到一组解，其对应的待优化目标函数值的点均落在上面的黑色加粗线上，那么就是我们想要的“帕累托最优解”了。此外，假如帕累托最优解个数不可数，那么我们只需找到上面黑色加粗线上的若干个点即可，并且这些点越分散、分布得越均匀，说明算法的效果越好。

多目标进化优化算法即利用进化算法结合多目标优化策略来求解多目标优化问题。经典而久经不衰的多目标优化算法有：NSGA2、NSGA3、MOEA/D等。其中NSGA2和NSGA3是基于支配的MOEA(Multi-objective evolutionary algorithm)，而MOEA/D是基于分解的MOEA。

前两者（NSGA2、NSGA3）通过非支配排序（后面马上讲到）来筛选出一堆解中的“非支配解”，并且通过种群的不断进化，使得种群个体对应的解对应的目标函数值的点不断逼近上图的黑色加粗线。具体算法就不作详细阐述了，可详见以下参考文献，或看下方的代码实战部分：

Deb K , Pratap A , Agarwal S , et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):0-197.

Deb K , Jain H . An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I:  Solving Problems With Box Constraints[J]. IEEE Transactions on  Evolutionary Computation, 2014, 18(4):577-601.

后者（MOEA/D）通过线性或非线性的方式将原多目标问题中各个目标进行聚合，即将多个目标聚合成一个目标，然后利用种群进化不断逼近全局帕累托最优解。这里可能有人会有疑问：“为什么MOEA/D是基于分解的MOEA，但过程中需要对各个目标进行聚合？那不就不叫分解了吗？”答案很简单：分解是指将多目标优化问题分解为一组单目标子问题或多个多目标子问题，利用子问题之间的邻域关系，通过协作来同时优化所有的子问题，从而不断逼近全局帕累托最优解；而聚合是指将多个目标聚合成一个目标，因此MOEA/D里面有“分解”和“聚合”两个步骤，分解是确定邻域关系，聚合是用来方便比较解的优劣，两者并不是矛盾的。具体算法就不作详细阐述了，可详见以下参考文献，或看下方的代码实战部分：

Qingfu Zhang, Hui Li. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[M]. IEEE Press, 2007.

那么存在只利用聚合而没有分解这一步来进化优化的算法吗？答案是存在的，比如多目标优化自适应权重法（awGA），代码详见链接：

https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/awGA/moea_awGA_templet.py

这个算法就是通过自适应地生成一个权重向量，来将所有的优化目标聚合成单一的优化目标，然后进行进化优化，当然这样效果自然比不上MOEA/D。

有些单目标优化学得比较溜的读者可能会疑问：”我找一组固定的权重，把各个优化目标加权聚合成一个目标，再用单目标优化的