最优化2：线性规划及单纯形法

文章作者：佚名浏览次数：发表时间：2024-07-01 13:27:47

本文旨在介绍线性规划的基本概念、单纯形算法和分析单纯形法背后的原理，参考资料包括Convex Optimization(by Stephen Boyd)，《最优化理论与算法(第2版)》(陈宝林编著)，维基百科以及其他在线资料等(详情见参考)。

线性规划(LP, Linear Programming)是指具有线性约束(包括等式约束和非等式约束)、线性目标函数的最优化问题。它是数学规划中极为特殊的一种形式。

其数学表达为

$\\begin{equation}\\begin{array}{ll}\ ext{ min }& c^{T}x \\\\ \ ext{ s.t. }& A x=b\\\\ \ ext{ }& Gx\\preceq h \\end{array}\\end{equation}$

特点：

可行域是一个凸集(包括空集)。因为其可行域有限多个半空间和超平面的交集，因此是一个多面体（前文已经说明多面体是一个凸集）。
目标函数既是凸函数，又是凹函数(因为是线性函数或仿射函数)

定理：

解的存在性定理^[1]。因为凸函数的最大值必在边界处取得，凹函数的最小值必在边界处取得。因此线性规划的目标函数的最小值和最大值都在边界处取得。因此线性规划的最优解(如果有的话)一定能在极点(vertices)处取得(当有多个最优解时，最优解的集合一定包含某个极点)。在两种情况下，LP无最优解：

LP不可行。即LP的约束自相矛盾，也即LP的可行域为空集。因为无可行解，自然也就没有最优解。
LP的可行域在目标函数梯度负方向无界(如果是最大化目标函数，则LP可行域在目标函数梯度方向无界)。在这种情况下，我们总能沿着负梯度方向找到更优的解，使得目标函数更小，因此无最优解。

多面体的极点和极方向。

定义(极点):

设 $S$ 为非空凸集， $x\\in S$ ，若 $x$ 不能表示为 $S$ 中两个不同点的严格凸组合，即 $x=\\lambda x^{(1)}+(1-\\lambda)x^{(2)}(\\lambda\\in(0,1))\\Longrightarrow x=x^{(1)}=x^{(2)}$ ,则称 $x$ 为凸集 $S$ 中的极点。

从几何上看，极点是凸集的边界的一点，包含该点且不以该点为端点的任意线段都不在这个凸集中。多面体的极点就是构成该多面体的超平面的交点。而圆上的每一点都是极点。

可以看出，有界集中任意一点都可以表示为极点的凸组合。但是对无界集却不成立，这时需要引入极方向的概念。

定义(极方向)：

设 $S$ 为闭凸集， $d$ 为非零向量，如果对 $S$ 中的每一个 $x$ ，都有射线

$\\{x+\\lambda d\\mid \\lambda \\geq 0\\}\\subset S$

则称 $d$ 为 $S$ 的方向。若 $d$ 不能表示为 $S$ 的两个不同方向的整的线性组合，则称 $d$ 为 $S$ 的极方向。

几何上，只有无界集才有方向。而极方向则是无界集的某个边界的方向向量。

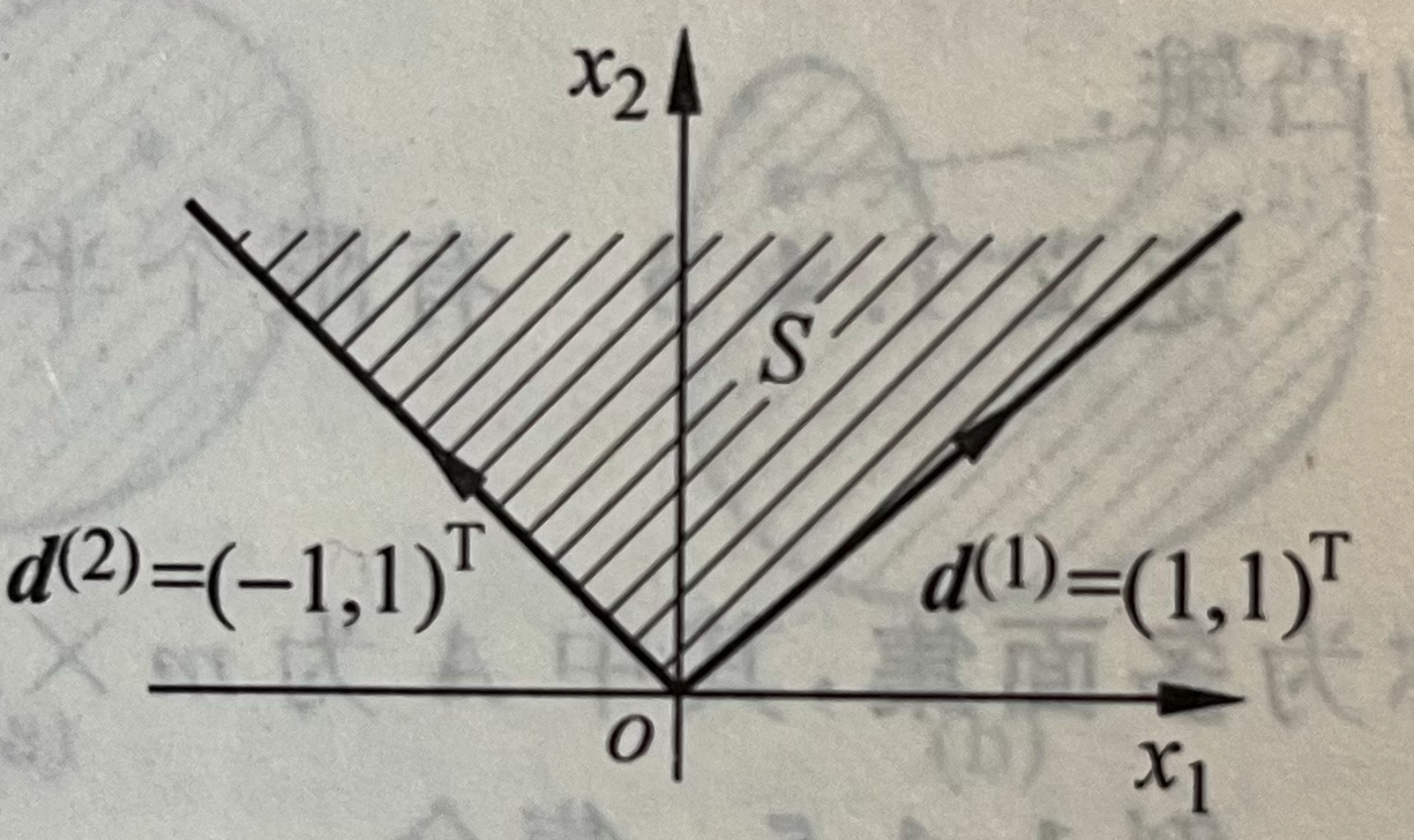
加上极方向后， $S$ 内的任意点可以用极点和极方向表示出来：

$x=\\sum_{j=1}^{k}\\lambda_jx^{(j)}+\\sum_{j=1}^{l}\\mu_jd^{(j)}\\\\ \\sum_{j=1}^k\\lambda_j=1\\\\ \\lambda_j\\geq0,\\ \\ j=1,\\dots,k,\\\\ \\mu_j\\geq0,\\ \\ j=1,\\dots,l$

即凸可行域中的任意一点都可以表示为极点的凸组合+极方向的锥组合。

一般的线性规划总是可以写成如下标准形式(通过添加松弛变量，将不等式约束变为等式约束，同时提升可行域的维度等方法)：

$\\begin{equation}\\begin{array}{ll}\ ext{ min }& c^{T}x \\\\ \ ext{ s.t. }& A x=b\\\\ \ ext{ }& x\\geq0 \\end{array}\\end{equation}$

其中 $A\\in \\mathbb{R}^{m\ imes n}_m$ , $x,c\\in\\mathbb{R}^n$ , $b\\in \\mathbb{R}^m,b\\succeq0$

化成标准形式的目的是便于引出基本可行解的概念和性质，进而为单纯形方法做铺垫。

我们引入基本可行解的目的是为了便于缩小最优解的范围。通过前面的分析，我们已经知道线性规划的最优解一定在极点处取得，因此只需找出极点的集合，则最优解一定在这个集合中。但是极点是个很强的几何概念，虽有直观的优势，但是它对于数值计算来说不太方便。因此，我们从数值上引入基本可行解的概念，并证明它与极点等价。基本可行解的代数含义很明确，便于演算。于是，我们将求解线性规划问题转变为求解可行域的极点问题，进而转换为求解基本可行解的问题。

接下来先给出基本可行解的定义，然后给出定理说明基本可行解与极点等价。

设 $A=(p_1,p_2,\\dots,p_n)$ ,已经假设矩阵 $A$ 的秩为 $m$ ，则必存在 $m$ 个线性无关的列向量。设这 $m$ 个列向量的下标组成的集合为 $S$ ；又设 $B$ 是 $A$ 中以 $S$ 的元素为下标的列向量构成的 $m\ imes m$ 方阵。设有点 $x$ ,它的以 $S$ 中元素作为下标的分量构成的列向量为 $x_B$ 。称 $B$ 为基矩阵， $x_B$ 称为一组基，各分量为基变量， $x$ 中其他分量为非基变量。令非基变量全为 $0$ ，则显然有 $x_B=B^{-1}b$ 。此时， $x$ 称为基本解(注意：基变量和非基变量在 $x$ 中的对应位置不变)。又若 $x$ 还满足不等式约束 $x\\succeq0$ ,称 $x$ 为基本可行解。(这段话比较绕，多读几遍)

至于基本解为什么要叫这个名字。个人认为“基”和线性空间里的“基”是类似的。还记得前面说的，紧的凸集中任何一个点都可以由极点线性表出吗？那么这里极点就相当于一个空间里的基(不严谨，但可以这样理解)，于是极点对应的解就称为基本解。

下面举一个例子来帮助理解基本可行解的概念：

例：设一个标准线性规划的等式约束为 $Ax=b$ ，其中 $\\begin{equation}A=\\left(\\begin{array}{lll}1 & 0 & 1 \\\\ 0 & 1 & 1 \\end{array}\\right) \\end{equation}$ , $\\begin{equation}b=\\left(\\begin{array}{l}1 \\\\ 0 \\end{array}\\right) \\end{equation}$ ,求解该线性规划的基本可行解。

解令 $A=(p_1,p_2,p_3)$ 。

令 $\\begin{equation}B=(p_1,p_2)=\\left(\\begin{array}{ll}1 & 0\\\\ 0 & 1 \\end{array}\\right) \\end{equation}$ , 解出 $x_B=B^{-1}b=\\begin{equation}\\left(\\begin{array}{l}1 \\\\ 0 \\end{array}\\right) \\end{equation}$ ，则 $\\begin{equation}x=\\left(\\begin{array}{l}1\\\\ 0\\\\ 0 \\end{array}\\right) \\end{equation}$
令 $\\begin{equation}B=(p_1,p_3)=\\left(\\begin{array}{ll}1 & 1\\\\ 0 & 1 \\end{array}\\right) \\end{equation}$ , 解出 $x_B=B^{-1}b=\\begin{equation}\\left(\\begin{array}{l}1 \\\\ 0 \\end{array}\\right) \\end{equation}$ ，则 $\\begin{equation}x=\\left(\\begin{array}{l}1\\\\ 0\\\\ 0 \\end{array}\\right) \\end{equation}$
令 $\\begin{equation}B=(p_2,p_3)=\\left(\\begin{array}{ll}0 & 1\\\\ 1 & 1 \\end{array}\\right) \\end{equation}$ , 解出 $x_B=B^{-1}b=\\begin{equation}\\left(\\begin{array}{l}-1 \\\\ 1 \\end{array}\\right) \\end{equation}$ ，则 $\\begin{equation}x=\\left(\\begin{array}{r}0\\\\ -1\\\\ 1 \\end{array}\\right) \\end{equation}$ , $x$ 不满足不等式约束 $x\\succeq0$ ，因此不是基本可行解。

所以本题中线性规划的基本可行解为 $\\begin{equation}x=\\left(\\begin{array}{l}1\\\\ 0\\\\ 0 \\end{array}\\right) \\end{equation}$ 。

几点发现：

根据基本可行解的概念，我们可以知道基本可行解最多可以有 $\\begin{equation}\\left(\\begin{array}{l}n \\\\ m \\end{array}\\right) \\end{equation}$ 个，因为从 $n$ 个列向量中选取 $m$ 个作为基的可能的选法有 $\\begin{equation}\\left(\\begin{array}{l}n \\\\ m \\end{array}\\right) \\end{equation}$ 个。
线性规划的基本可行解只与系数矩阵 $A$ 和偏置 $b$ 有关。
基本可行解中正分量的个数不超过系数矩阵的秩。

定理：令 $K=\\{x|Ax=b,x\\succeq 0\\}$ , $A$ 是 $m\ imes n$ 矩阵，秩为 $m$ 。则 $K$ 的极点集与 $Ax=b,x\\succeq 0$ 的基本可行解等价。

这里不给出严格证明，只描述证明思路：分别证明充分性和必要性。

已知 $x$ 是极点，证明 $x$ 是基本可行解。设 $x$ 有 $s$ 个正分量，先证明 $x$ 的正分量对应的 $A$ 中的列向量线性无关，由此说明 $x$ 的正分量个数 $s$ 小于等于 $m$ 。然后其他 $m-s$ 个列向量与这 $s$ 个列向量组成基矩阵 $B$ ， $x$ 相应的拆分为 $x_B$ 和其他非基变量(都是0)。由此可得 $x_B=B^{-1}b$ ，因此 $x$ 是基本可行解。
已知 $x$ 是基本可行解，证明 $x$ 是极点。设 $x^{(1)},x^{(2)}$ 分别为可行解，且 $x$ 是它们的凸组合。因为 $x$ 有 $m-s$ 个分量为 $0$ ，则 $x^{(1)},x^{(2)}$ 对应的分量也必须为0(因为正数的凸组合必大于0)。再根据 $Ax^{(1)}=b,Ax^{(2)}=b,$ 得到 $x_B^{(1)}=x_B^{(2)}=B^{-1}b=x_B$ ,从而 $x=x^{(1)}=x^{(2)}$ 。因此 $x$ 是极点。

有了这个定理，我们可以将求解极点问题转换为求解基本可行解问题。然后再基本可行解集中寻找最优解。即，线性规划问题的求解，可归结为求最优基本可行解。这也正是单纯形方法的基本出发点。

直接给出定理而不加证明。

定理：如果 $Ax=b,x\\succeq0$ 有可行解，则一定存在基本可行解。

上文已经探讨了线性规划最优解与基本可行集的关系，即如果线性规划具有最优解，它一定能在基本可行解中找到。我们可以先找到所有的基本可行解，然后代入目标函数，寻找最大值。然而，一个 $m\ imes n$ 的系数矩阵可能有多达 $\\begin{equation}\\left(\\begin{array}{l}n \\\\ m \\end{array}\\right) \\end{equation}$ 个基本可行解，如果 $n>>m$ ，那么时间复杂度会很高。所以应该改良这种暴力算法，采用一种更高效的方法。这就是成熟的单纯形法(Simplex Algorithm or Simplex Method)。

这部分内容不打算按照课本那样用定理和公式来解释单纯形法(但是重要的推导还是有必要的)，而是着重于剖析其原理。由于“基本可行解”和“极点”的定价性，下文可能将二者混用，以便更好地理解。

首先介绍单纯形法的思想：相对于暴力算法，单纯形法从一个基本可行解切换到另一个基本可行解时，不是盲目的切换。首先，它只会沿着边(edge)切换到与它相邻的极点。其次，它只会切换到能改良优化目标的极点。重复这样的做法，直到再也找不到能改良优化目标的相邻极点时，此刻所在的极点就是本次线性规划的最优解。这种做法的合理性基于以下事实：若一个极点不是线性规划的最优解，则它的一个相邻极点比它更优。

那什么样的相邻极点是更好的呢？不妨设此时所在的极点是 $x^{(0)}$ ，它的一个相邻极点是 $x^{(1)}$ 。则如果 $x^{(1)}-x^{(0)}$ 的方向与目标函数的负梯度方向成锐角，那么 $x^{(1)}$ 一定比 $x^{(0)}$ 更优(这是显然的)。用数学公式描述为 $\ abla f^T(x^{(1)}-x^{(0)})<0$ 。

我们就以该不等式为出发点探究 $x^{(1)}$ 应满足什么条件。

首先，规定一些符号。从 $x^{(0)}\\in \\mathbb{R^n}$ 中抽取其所有基变量组成 $m$ 维向量 $x^{(0)}_B \\in \\mathbb{R^m}$ ,剩余的非基变量组成 $n-m$ 维向量 $x^{(0)}_N=0_{n-m}\\in \\mathbb{R}^{n-m}$ （基本可行解的非基变量都是零）。类似地，分别从 $c^T\\in \\mathbb{R^n},A\\in\\mathbb{R}^{m\ imes n}$ 中抽取出 $c^T_B\\in \\mathbb{R^m},c^T_N\\in \\mathbb{R^{m-n}},B\\in \\mathbb{R}^{m\ imes m},N\\in \\mathbb{R}^{m\ imes (n-m)}$ 。然后从 $x^{(1)}$ 中抽取与 $x^{(0)}$ 相同位置的变量 $x^{(1)}_B \\in \\mathbb{R^m}$ , $x^{(1)}_N\\in \\mathbb{R}^{n-m}$ 。

强调一下， $x^{(1)}_B$ 不是代表 $x^{(1)}$ 的基变量组成的向量，它只是代表和 $x^{(0)}_B$ 位置而已，同样 $x^{(1)}_N$ 也不是零向量(后面会说它的含义)。

下面正式开始推导。

$\\begin{equation}\\begin{split}&\ abla f^T(x^{(1)}-x^{(0)}) \\\\ &=c^Tx^{(1)}-c^Tx^{(0)}\\\\ &=c^T_Bx^{(1)}_B+c^T_Nx^{(1)}_N-(c^T_Bx^{(0)}_B+c^T_Nx^{(0)}_N)\\\\ &=( c^T_BB^{-1}b-c^T_BB^{-1}Nx_N^{(1)}+c^T_Nx^{(1)}_N)-(c^T_BB^{-1}b)\\\\ &=(-c^T_BB^{-1}N+c^T_N)x^{(1)}_N<0\\\\ \\iff& (c^T_BB^{-1}N-c^T_N)x^{(1)}_N>0 \\end{split}\\end{equation}$

注意 $x^{(1)}$ 是任取的。也就是说，只要满足 $(c^T_BB^{-1}N-c^T_N)x^{(1)}_N>0$ 就说明还有优化空间,即从 $x^{(0)}$ 切换到 $x^{(1)}$ ；否则，意味着 $x^{(0)}$ 就是该问题的最优解。

问题转变为我们从当前极点，挑选满足不等式 $(c^T_BB^{-1}N-c^T_N)x^{(1)}_N>0$ 的相邻极点，然后切换到该极点就完成了一次优化的迭代。那如果多个极点满足该条件呢？理论上我们应该取 $(c^T_BB^{-1}N-c^T_N)x^{(1)}_N$ 最大的那个。可是，这要求要找出当前极点的所有相邻极点，也需要很大的计算量(虽然比暴力解法确实进步了)。所以，可以退而求其次，取使 $(c^T_BB^{-1}N-c^T_N)$ 最大的就行，因为这个是不需要其他极点就能计算的。

在继续讨论之前，我们给出 $x^{(1)}_N$ 的含义。我们知道当从一个极点移动到另一个极点时，非基变量中有且仅有一个会从0增加到一个正值。由于 $x^{(0)},x^{(1)}$ 是相邻极点， $x^{(0)}_N$ 是0向量，所以 $x^{(1)}_N$ 中有一个元素为正值，其余全是0。

现在来探究一下 $(c^T_BB^{-1}N-c^T_N)x^{(1)}_N>0$ 意味着什么。

将不等式写成分量形式： $\\sum_{j\\in R}(c^T_BB^{-1}p_j-c_j)x_j>0$ ，其中 $R$ 是非基变量的下标集合。再设 $x^{(1)}_N$ 中不为0的元素下标为 $k$ ，则不等式可进一步化简为 $(c^T_BB^{-1}p_k-c_k)>0,k\\in R$ 。令 $\\sigma_k=c^TB^{-1}p_k-c_k$ ,称为判别数。

所以这个不等式的意思其实是：如果当前所在极点存在某个属于非基变量下标集合的下标 $k$ ,它对应的各参数满足这个不等式，那么我们可以让 $p_k$ 成为新的基矩阵的元素，这个基矩阵对应的基本可行解优于当前可行解。

那如果有多个下标 $k$ 满足该不等式呢？当然是选取 $\\max\\{\\sigma_k>0,k\\in R\\}$ 。注意，我们没有计算所有的相邻极点，而是根据 $x^{(1)}_N$ 的特殊结构，计算出所有的相邻极点对应的判别数 $\\sigma_k$ ，再取它们中最大的对应的下标，作为新入基列的下标。有列入基，就有列出基，因为基矩阵只容纳 $m$ 个列。那应该怎么选择出基的那一列呢？

为了便于说明，先将问题作一个化简：我们令 $B=I$ 。这总是可以通过行初等变换做到，相应的 $N,b$ 也同时做一样的行初等变换以保持解不变。这样变换后的 $b$ 的值就是基变量的取值（如果 $b$ 经过行初等变换后有负的元素，那就说明这个基矩阵对应的基本解不可行，应该重新寻找基矩阵）。当有新列入基时，我们将该列变换为 $I$ 中的某一列，即只有一个元素为1，其余元素都为0；然后，与新列重复的那一列出基。那么我们应该将新列的哪个元素(主元)变换为1呢？设新列的第 $r$ 个元素为 $p_{kr}$ ，取 $\\min _r\\{\\frac{b_r}{p_{kr}}>0\\}$ 对应的那个下标。因为只有这样才能保证在行初等变换时，不会把 $b$ 中的元素消为负数。还有一个问题是，如果新入基列 $p_k$ 中所有元素都小于等于0呢？这样的话， $\\min _r\\{\\frac{b_r}{p_{kr}}>0\\}$ 是不存在的(因为 $b_r$ 必定非负)。实际上，出现了这样情况说明该线性规划问题无最优解(目标函数可以任意小)。

介绍完单纯形方法的原理，步骤也就呼之欲出了。这里简要做一个总结。

将线性规划问题转换为标准形式
在系数矩阵 $A$ 中寻找一个基矩阵 $B$ ，并通过行初等变换将它转换为单位矩阵 $I$ 。如果此时 $b\ succeq0$ ，则重新寻找基矩阵并转换为单位阵，直到 $b\\succeq0$ 。
计算 $N$ 中每一列对应的判别数 $\\sigma_j=c^TB^{-1}p_j-c_j=c^Tp_j-c_j$ ，然后取 $\\sigma_k=\\max_j\\{\\sigma_j\\}$ 。如果 $\\sigma_k\\leq0$ ，则当前基本可行解就是最优解，算法停止。否则，若 $p_k\\preceq0$ ，则说明线性规划无最优解，算法停止。否则，选择 $p_k$ 作为入基列。
计算 $\\min_r\\{\\frac{b_r}{p_{kr}}>0\\}$ 对应的 $r$ ，将 $p_{kr}$ 作为主元，通过行初等变换将主元化为1，其余元素化为0，实际完成了入基。返回步骤3。

PS: 操作过程中，一定要注意各参数的对应。比如如果基矩阵 $I=(p_2,p_5,p_1)$ ，那么相应的 $x_B^T=(x_2,x_5,x_1),c^T_B=(c_2,c_5,c_1)$ ，而不是简单得按照顺序取 $x^T_B=(x_1,x_2,x_5)$ 等等。

上面给出了单纯形方法的原理和步骤，对线性规划问题给出了一个成熟优雅的方案。但是，还是有一点小瑕疵，那就是单纯形方法的第一步：寻找初始的基本可行解。如果系数矩阵 $A$ 中存在能组成单位矩阵的列向量，那就很完美，我们已经找到了一个基本可行解。但若不存在单位矩阵呢？一般情况下，很难直接看出哪些列是线性无关的。因此，我们需要人为地构造出一个单位矩阵来提供初始的基本可行解。两阶段法和大M法提供了这样的功能。本小节简要介绍两阶段法；下一节简要介绍大M法。

在一个标准线性规划问题中，一般不存在现成的单位矩阵，两阶段法通过引入人工变量 $0\\preceq x_a\\in\\mathbb{R}^m$ ，将 $x_a$ 的每个元素添加到每个方程中，等价于在 $A$ 右端增加了一个单位向量 $I$ 。但是这个做法已经破坏了方程组的结构，没关系，后续的处理(即第一阶段)会讲人工变量逼出基变量，从而消除这个不好影响。

求解一下线性优化问题，以消除人工变量的影响：

$\\begin{equation}\\begin{array}{ll}\ ext{ min }& e^{T}x_a \\\\ \ ext{ s.t. }& A x+x_a=b\\\\ \ ext{ }& x\\succeq0\\\\&x_a\\succeq0 \\end{array}\\end{equation}$

其中 $e^T=(1,1,\\dots,1)$ 。

因为有初始基本可行解，且目标函数有下届，所以必存在最优基本可行解，设为 $\\begin{equation}\\begin{split}\\left[ \\begin{array}{c}x\\\\ x_a \\end{array}\\right]\\end{split}\\end{equation}$ 。此时，有三种情况：

$x_a\ e 0$ ，则原线性规划无可行解。因为若原线性规划有可行解，则 $\\begin{equation}\\begin{split}\\left[ \\begin{array}{c}x\\\\ x_a \\end{array}\\right]=\\left[ \\begin{array}{c}\\hat{x}\\\\ 0 \\end{array}\\right]\\end{split}\\end{equation}$ 是这个线性规划的可行解，则目标函数可以取0，矛盾。
$x_a=0$ 且 $x_a$ 的分量都是非基变量。则 $m$ 个基变量都是原线性规划的基变量。
$x_a=0$ 且 $x_a$ 的某些分量是基变量。这时可以使用主元消去法，将这些元素离基，得到不含人工变量的基变量。

用第一阶段得到的基，求解原线性规划问题。

大M法和两阶段法类似，都是通过引入人工变量构造单位矩阵，然后迫使人工变量离基。但大M法只需要一个阶段，它的思想是在目标函数上加上很大的倍数M的人工变量的惩罚项，在优化过程中使人工变量必须为0。大M法其实是两阶段法中两个阶段的结合。

大M法求解以下线性规划问题。

$\\begin{equation}\\begin{array}{ll}\ ext{ min }& c^Tx+Me^{T}x_a \\\\ \ ext{ s.t. }& A x+x_a=b\\\\ \ ext{ }& x\\succeq0\\\\&x_a\\succeq0 \\end{array}\\end{equation}$

其结果必是下面三种情况之一：

达到线性规划最优解，且 $x_a=0$ ,则此时 $x$ 就是原线性规划最优解。
达到线性规划最优解，且 $x_a\ e 0$ ，则原线性规划问题无可行解。
不存在有限最优值，则原线性规划问题无界或无可行解。

下一篇：篮球网什么材质的好篮球框网的材质对投篮有影响吗上一篇：戈者设计_2

400-123-4567

最优化2：线性规划及单纯形法

推荐产品

热门文章排行

最新资讯文章